Karel Lambert

Karel Lambert (born 1928) is a philosopher and logician at the University of California, Irvine and the University of Salzburg. He has written extensively on the subject of free logic, a term which he coined^[1].

Lambert's Law

Lambert's Law is the adjustment of a given standard predicate logic such as to relieve it of existential assumptions, and so make it a free logic. Taking Bertrand Russell's predicate logic in his Principia Mathematica as standard, one replaces universal instantiation, 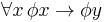, with universal specification 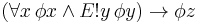. Thus universal statements, like "All men are mortal," or "Everything is a unicorn," do not presuppose that there are men or that there is anything. These would be symbolized, with the appropriate predicates, as 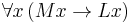and 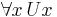, which in Principia Mathematica entail 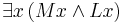and 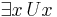, but not in free logic. The truth of these last statements, when used in a free logic, depend on the domain of quantification, which may be the null set.

Published works

• Philosophical Applications of Free Logic "A Theory of Definite Descriptions" (1991) details an account of Russell's Theory of Descriptions in free logic. In the process, he demonstrates how a formulation from Hintikka allows for a contradiction by a correlate in logic to Russell's Paradox. He introduces the predicate

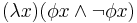
External links

• Official Personal Page at Internet Archive

References

1. ^ Lambert, Karel (1960). "The Definition of E! in Free Logic". Abstracts: The International Congress for Logic, Methodology and Philosophy of Science (Palo Alto, CA: Stanford University Press).